- Draw pictures of all nonisomorphic 6-node trees.
- Prove that there are at least
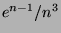 distinct isomorphism types of
distinct isomorphism types of 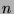 -node trees.
(Hint: Apply the Sylvester-Cayley tree counting
theorem and the inequality
-node trees.
(Hint: Apply the Sylvester-Cayley tree counting
theorem and the inequality
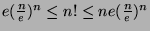 .)
.)
- Every tree with at least two nodes contains at least two leaves.
- Let
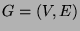 be an arbitrary graph, and
be an arbitrary graph, and 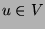 a leaf
(= node of degree 1) in
a leaf
(= node of degree 1) in 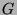 . Then
. Then 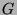 is a tree, if and
only if the graph
is a tree, if and
only if the graph 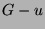 (= the subgraph of
(= the subgraph of 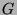 spanned by
nodes
spanned by
nodes
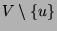 ) is a tree.
) is a tree.
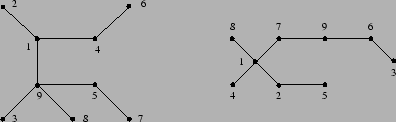
- Draw pictures of the graphs
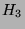 and
and 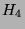 .
How many nodes are there in graph
.
How many nodes are there in graph 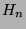 ?
?
- For which values of
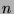 does
does 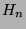 contain a closed Eulerian tour?
contain a closed Eulerian tour?
- Determine the diameter of graph
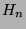 ,
i.e. the biggest possible internode distance in
,
i.e. the biggest possible internode distance in 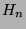 ,
,
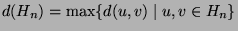 ,
where the distance
,
where the distance 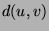 between nodes
between nodes 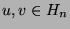 is defined as the length of the shortest path connecting them.
is defined as the length of the shortest path connecting them.
(Note: The Hamiltonian cycles of hypercube ![]() correspond to so called cyclic Gray codes of the integers
0, ...,
correspond to so called cyclic Gray codes of the integers
0, ..., ![]() . These have the property
that the binary representations of any two consequent
numbers differ in exactly one bit.)
. These have the property
that the binary representations of any two consequent
numbers differ in exactly one bit.)