


Next: About this document ...
Up: prob1
Previous: prob1
- The Fibonacci numbers
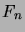 ,
, 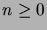 , are defined by
the recurrence relation
, are defined by
the recurrence relation 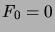 ,
, 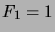 ,
,
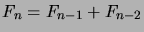 , for
, for 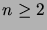 .
(Thus the first numbers in the sequence are 0, 1, 1, 2, 3, 5, 8, ...)
Prove by induction on
.
(Thus the first numbers in the sequence are 0, 1, 1, 2, 3, 5, 8, ...)
Prove by induction on 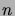 that for all
that for all 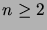 ,
,
where 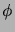 denotes the ``golden ratio''
denotes the ``golden ratio''
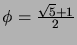 .
.
- Let
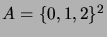 . Draw the Hasse diagram of the order relation
. Draw the Hasse diagram of the order relation
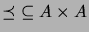 , where
, where
(Here  denotes the standard ordering of the integers.)
Is the corresponding relation, where ``and'' is replaced by ``or''
in the definition, also a partial order?
denotes the standard ordering of the integers.)
Is the corresponding relation, where ``and'' is replaced by ``or''
in the definition, also a partial order?
- List all the equivalence relations (partitions) on
the set
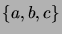 .
.
- Draw the Hasse diagrams of all the (partial) orders
on the set
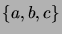 .
.
- Describe, in a general way, the structure of the ordered sets
 and
and
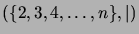 .
(The notation ``|'' here denotes the divisibility relation
of the integers, i.e.
.
(The notation ``|'' here denotes the divisibility relation
of the integers, i.e. 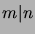 iff
iff 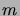 is a factor of
is a factor of 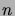 .)
What are the minimal elements of the orders? Immediate successors
of a given element? What is the maximal length in each order of
a chain, i.e. a totally ordered sequence of elements
.)
What are the minimal elements of the orders? Immediate successors
of a given element? What is the maximal length in each order of
a chain, i.e. a totally ordered sequence of elements
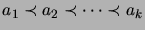 ?
?
- Prove that every finite ordered set contains a maximal,
but not necessarily a greatest element.
- The induction principle for natural numbers claims that
the following holds for any property
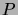 of the natural numbers:
if
of the natural numbers:
if 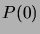 is true, and the implication
is true, and the implication
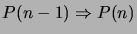 is true for all
is true for all
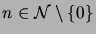 , then
, then 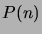 is true
for all
is true
for all
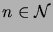 .
Prove the correctness of this principle, using the facts that
the standard ordering of the natural numbers
.
Prove the correctness of this principle, using the facts that
the standard ordering of the natural numbers
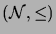 is a well-ordering with least element
is a well-ordering with least element 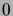 , and in addition
every element
, and in addition
every element
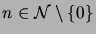 has an immediate
predecessor
has an immediate
predecessor 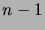 .
.



Next: About this document ...
Up: prob1
Previous: prob1
Pekka Orponen
2000-09-25
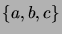 .
.
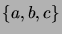 .
.