- Piirrä kaikki keskenään ei-isomorfiset 6-solmuiset puut.
- Osoita, että
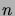 -solmuisten puiden isomorfiatyyppejä
on ainakin
-solmuisten puiden isomorfiatyyppejä
on ainakin 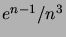 kappaletta. (Ohje:
Sovella Sylvesterin-Cayleyn lausetta ja epäyhtälöä
kappaletta. (Ohje:
Sovella Sylvesterin-Cayleyn lausetta ja epäyhtälöä
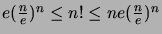 .)
.)
- Jokaisessa vähintään kaksisolmuisessa puussa on ainakin kaksi lehteä.
- Olkoon
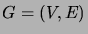 mielivaltainen verkko ja
mielivaltainen verkko ja 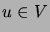 jokin
jokin 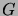 :n
lehti (= solmu, jonka asteluku on 1). Tällöin
:n
lehti (= solmu, jonka asteluku on 1). Tällöin 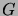 on puu, jos
ja vain jos verkko
on puu, jos
ja vain jos verkko 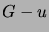 (= solmujoukon
(= solmujoukon
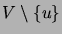 virittämä
virittämä
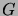 :n aliverkko) on puu.
:n aliverkko) on puu.
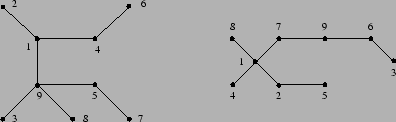
- Piirrä verkot
 ja
ja 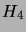 . Montako solmua on verkossa
. Montako solmua on verkossa 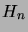 ?
?
- Millä
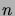 :n arvoilla verkko
:n arvoilla verkko 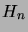 sisältää Eulerin kierroksen?
sisältää Eulerin kierroksen?
- Määritä verkon
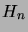 halkaisija, so. suurin mahdollinen
kahden solmun välinen etäisyys
halkaisija, so. suurin mahdollinen
kahden solmun välinen etäisyys
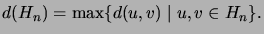 (Solmujen
(Solmujen 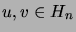 välinen etäisyys
välinen etäisyys 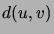 tarkoittaa lyhimmän niitä yhdistävän polun pituutta.)
tarkoittaa lyhimmän niitä yhdistävän polun pituutta.)
(Huomautus: Hyperkuution ![]() Hamiltonin kehät vastaavat
kokonaislukujen 0, ...,
Hamiltonin kehät vastaavat
kokonaislukujen 0, ..., ![]() ns. syklisiä Gray-koodeja,
joissa kahden peräkkäisen luvun binääriesitykset poikkeavat
aina vain yhdessä bitissä.)
ns. syklisiä Gray-koodeja,
joissa kahden peräkkäisen luvun binääriesitykset poikkeavat
aina vain yhdessä bitissä.)