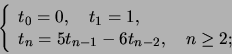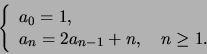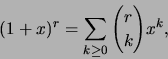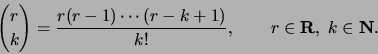Next: Tästä dokumentista ...
Up: harj4
Previous: harj4
- Portaikossa voi nousta 1 tai 2 askelmaa kerrallaan. Laadi
rekursioyhtälö, joka kuvaa montako
erilaista tapaa on nousta ylös
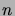 -askelmainen portaikko.
(Ohje: Osita
-askelmainen portaikko.
(Ohje: Osita 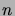 -askelmaisen portaikon nousutavat
sen mukaan, noustaanko 1. askelella 1 vai 2 askelmaa.)
-askelmaisen portaikon nousutavat
sen mukaan, noustaanko 1. askelella 1 vai 2 askelmaa.)
- Ratkaise seuraavat rekursioyhtälöt karakterististen
polynomien tekniikalla:
-
-
- Olkoon
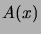 lukujonon
lukujonon
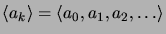 generoiva funktio ja
generoiva funktio ja
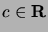 ,
,
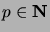 vakioita.
Minkä lukujonojen generoivia funktioita ovat seuraavat:
vakioita.
Minkä lukujonojen generoivia funktioita ovat seuraavat:
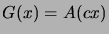 ,
,
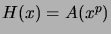 ,
,
-
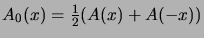 ja
ja
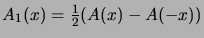 ?
?
- Muodosta seuraavien lukujonojen generoivat funktiot:
-
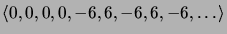 ;
;
-
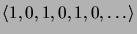 ;
;
-
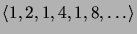 ;
;
-
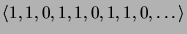 .
.
- Newtonin (yleistetyn) binomikaavan mukaan on kaikilla
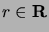 ja
ja 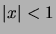 voimassa:
voimassa:
missä yleistetty binomikerroin
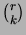 määritellään:
määritellään:
Lisäksi määritellään
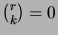 , kun
, kun 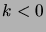 .
Todista seuraavat yleistettyjen binomikertoimien ominaisuudet:
.
Todista seuraavat yleistettyjen binomikertoimien ominaisuudet:
-
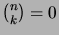 , kun
, kun
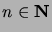 ja
ja 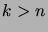 ;
;
-
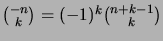 , kun
, kun
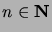 ;
;
-
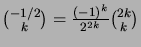 ,
,
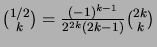 .
.
- Minkä lukujonojen generoivia funktioita ovat
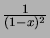 ja
ja
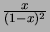 ? (Vihje: Sovella edellisen tehtävän
tuloksia.)
? (Vihje: Sovella edellisen tehtävän
tuloksia.)
- Ratkaise tehtävän 2(b) rekursioyhtälö generoivien funktioiden
avulla.



Next: Tästä dokumentista ...
Up: harj4
Previous: harj4
Pekka Orponen
2000-10-16
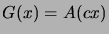 ,
,
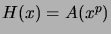 ,
,
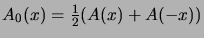 ja
ja
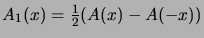 ?
?
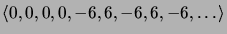 ;
;
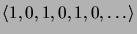 ;
;
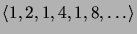 ;
;
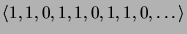 .
.
 , kun
, kun
 ja
ja 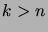 ;
;
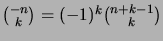 , kun
, kun
 ;
;
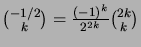 ,
,
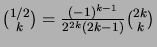 .
.