


Next: Tästä dokumentista ...
Up: harj1
Previous: harj1
- Fibonaccin luvut
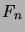 ,
, 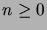 , määritellään
kaavoilla
, määritellään
kaavoilla 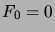 ,
, 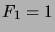 ,
,
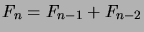 , kun
, kun 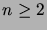 .
(Lukusarjan ensimmäiset luvut ovat siis 0, 1, 1, 2, 3, 5, 8, ...)
Todista induktiolla indeksin
.
(Lukusarjan ensimmäiset luvut ovat siis 0, 1, 1, 2, 3, 5, 8, ...)
Todista induktiolla indeksin 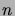 suhteen, että kaikilla
suhteen, että kaikilla 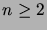 on voimassa
on voimassa
missä luku 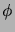 on ns. ``kultaisen leikkauksen suhde''
on ns. ``kultaisen leikkauksen suhde''
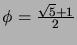 .
.
- Olkoon
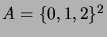 . Piirrä Hasse-kaavio järjestysrelaatiosta
. Piirrä Hasse-kaavio järjestysrelaatiosta
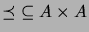 , missä
, missä
(Tässä siis relaatio  on kokonaislukujen tavanomainen järjestys.)
Onko vastaava relaatio, jonka määrittelyssä on ``ja''-sana korvattu
``tai''-sanalla, myös osittainjärjestys?
on kokonaislukujen tavanomainen järjestys.)
Onko vastaava relaatio, jonka määrittelyssä on ``ja''-sana korvattu
``tai''-sanalla, myös osittainjärjestys?
- Luettele kaikki joukon
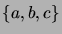 ekvivalenssirelaatiot (ositukset).
ekvivalenssirelaatiot (ositukset).
- Piirrä kaikkien joukon
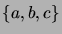 järjestysrelaatioiden (osittainjärjestysten) Hasse-kaaviot.
järjestysrelaatioiden (osittainjärjestysten) Hasse-kaaviot.
- Kuvaile yleisesti järjestettyjen
joukkojen
 ja
ja
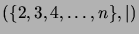 rakennetta. (Merkintä ``|'' tarkoittaa
tässä kokonaislukujen jaollisuusrelaatiota:
rakennetta. (Merkintä ``|'' tarkoittaa
tässä kokonaislukujen jaollisuusrelaatiota: 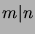 , jos
, jos 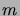 on
on 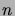 :n
tekijä.) Mitkä ovat järjestysten
minimialkiot? Annetun alkion välittömät seuraajat? Miten pitkä voi
kummassakin järjestyksessä olla maksimaalisen pitkä ketju, so. täydellisesti järjestetty alkiojono
:n
tekijä.) Mitkä ovat järjestysten
minimialkiot? Annetun alkion välittömät seuraajat? Miten pitkä voi
kummassakin järjestyksessä olla maksimaalisen pitkä ketju, so. täydellisesti järjestetty alkiojono
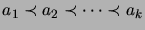 ?
?
- Osoita, että jokainen äärellinen järjestetty joukko
sisältää maksimaalisen, mutta ei välttämättä suurinta
alkiota.
- Luonnollisten lukujen induktioperiaatteen mukaan mille
tahansa luonnollisten lukujen ominaisuudelle
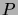 on voimassa,
että jos
on voimassa,
että jos 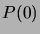 on tosi ja implikaatio
on tosi ja implikaatio
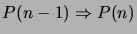 on tosi kaikilla
on tosi kaikilla
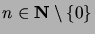 ,
niin
,
niin 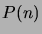 on tosi kaikilla
on tosi kaikilla
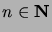 .
Todista periaate oikeaksi lähtien tiedoista, että
luonnollisten lukujen suuruusjärjestys
.
Todista periaate oikeaksi lähtien tiedoista, että
luonnollisten lukujen suuruusjärjestys
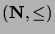 on
hyvinjärjestys, jolla on pienin alkio
on
hyvinjärjestys, jolla on pienin alkio 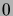 , ja lisäksi jokaisella
alkiolla
, ja lisäksi jokaisella
alkiolla
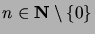 on välitön edeltäjä
on välitön edeltäjä 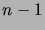 .
.



Next: Tästä dokumentista ...
Up: harj1
Previous: harj1
Pekka Orponen
2000-10-05
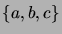 ekvivalenssirelaatiot (ositukset).
ekvivalenssirelaatiot (ositukset).
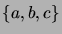 järjestysrelaatioiden (osittainjärjestysten) Hasse-kaaviot.
järjestysrelaatioiden (osittainjärjestysten) Hasse-kaaviot.